Korki zDolnego Śląska [LEKCJE ONLINE, ZADANIA, ZAGADKI]

Podsumowanie wszystkich zajęć:

Naszymi nauczycielami byli Zbigniew Lis i Kamil Braksator, nauczyciele z IX LO we Wrocławiu. 

Podsumowanie zajęć z matematyki:

Podsumowanie zajęć z fizyki:

Zadanie dla Słuchaczy na 6 maja:

W pudełku jest 10 kul białych, 20 czerwonych, 30 zielonych. Mam przepaskę na oczach i losuję po kolei kule. Ile ich najmniej muszę wyciągnąć, aby mieć pewność, że są wśród nich:

a) dwie kule tego samego koloru?
b) trzy kule tego samego koloru?

Odpowiedź to 4 i 7. 

Najpierw zapytaliśmy o to sportowców i muzyków. Jak oni sobie poradzili? Posłuchajcie:

A teraz wytłumaczenie:

Lekcja fizyki - 6 maja. Zadania przygotował nasz stały gość - Kamil Braksator, nauczyciel IX LO we Wrocławiu:

Prąd elektryczny:

Zadanie 1.

Kontakt z nieizolowanym przewodem nadpowietrznej sieci energetycznej jest dla człowieka bardzo niebezpieczny. Dlaczego więc prąd elektryczny nie poraża ptaków siedzących na przewodach?

Zadanie 2.

Ile dżuli zawiera kWh.

Zadanie 3.

a) Oblicz natężenie prądu, jaki płynie przez żarówkę o mocy P1= 100 W pod napięciem U1= 230 V.
b) Jaki jest opór tej żarówki?
c) Jak zmieni się moc wydzielana na tej żarówce, gdybyśmy ją podłączyli do napięcia U2=115 V?

Zadanie 4.

Ile oporników o oporze 24 Ω każdy trzeba połączyć równolegle, aby ich opór zastępczy był równy 1Ω

Zadanie 5. Zadanie domowe

Akumulator samochodowy ma pojemność 45 Ah. Ile to kulombów.

Odpowiedzi:

Zadanie 1.

Gdy człowiek dotknie takiego przewodu, popłynie przez niego między przewodem a ziemią prąd o natężeniu zależnym od wielkości oporu ciała człowieka i materiałów które znajdują się na drodze prądu, oraz od wielkości napięcia elektrycznego między przewodem a ziemią. Przeważnie jest to dla człowieka niebezpieczne. Ptak siedzący na przewodzie pod napięciem nie jest połączony z ziemią, więc nie przepływa przez niego prąd o dużym natężeniu. W sensie elektrycznym można potraktować ptaka jak opór elektryczny podłączony równolegle do przewodu w punktach gdzie z przewodem stykają się nóżki ptaka. Część prądu przepływa przez ciało ptaka. Opór ciała ptaka jest wielokrotnie większy od oporu odcinka przewodu między jego nóżkami. Dlatego też przez ciało ptaka popłynie bardzo małe natężenie prądu. Prąd jest tak mały, że ptak nie reaguje na jego działanie.

Zadanie 2.

1 godzina to 60 minut, każda minuta ma 60 sekund wobec tego 1 godzina to 3600 s. Zatem, możemy zapisać:
1 kWh= 1000*3600 Ws= 3600000Ws=3600000 J

Zadania 3.

a)
P=I*U
I=P/U
I=100/230=0,43 A

b)
P=I*U
I=U/R
Na podstawie tych dwóch wzorów otrzymujemy dwa dodatkowe wzory na moc:
P=I2*R, oraz P=U2/R
W zadaniu mamy podane napięcie oraz moc zatem przekształcamy ten drugi wzór do postaci:
R=U2/P =2302/100=529Ω

c)
Przy założeniu, że opór nie ulega zmianie na podstawie wzoru P=U2/R, widzimy, że moc jest proporcjonalna do napięcia podniesionego do potęgi drugiej. Jeżeli żarówka zamiast do napięcia 230 V została podłączona do napięcia 115 V, czyli napięcia dwukrotnie mniejszego to wydzielana moc zmaleje aż czterokrotnie .

Zadanie 4.

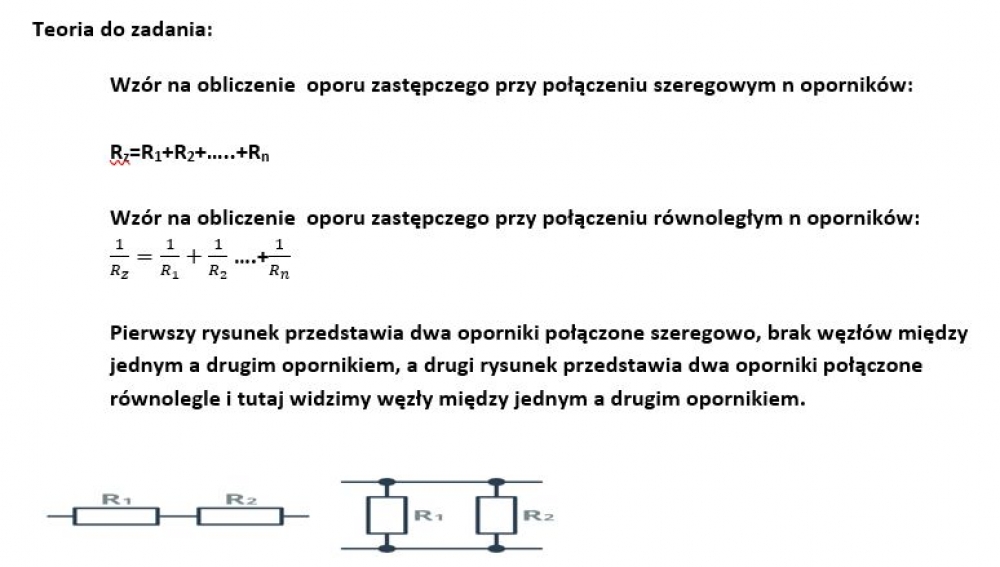
W naszym przypadku wykorzystujemy wzór na połączenie równoległe. Na podstawie wzoru widzimy, że aby uzyskać 1 Ω należy uzyskać iloraz 24/24. Dlatego należy połączyć 24 takie oporniki równolegle aby uzyskać opór zastępczy 1Ω

Podpowiedź do zadania 5

Natężeniem prądu nazywamy iloraz ładunku przepływającego przez poprzeczny przekrój przewodnika do czasu, w którym ten ładunek przepłynął: I=q/t

Zbigniew Lis, nauczyciel matematyki z IX LO we Wrocławiu, omawiał zadania, których nie zdążyliśmy tydzień temu:

Zadanie dla Słuchaczy na 29 kwietnia:

Mamy 100 złotych i za nie musimy kupić 100 zwierząt. Sarny są po 10 zł, zające po 3 zł., kuropatwy po 50 gr. Musi być spełniony warunek: 100 zł wydane i kupione 100 zwierząt.

Jakie zwierzęta kupimy?

Jak z tym pytaniem poradzili sobie Słuchacze i celebryci? 

A oto rozwiązanie:

Odpowiedź:

5 saren
1 zając
94 kuropatwy

Zbigniew Lis, nauczyciel matematyki z IX LO we Wrocławiu, przygotował nowe zadania:

Zadania:

1. Odległość między miastami A i B wynosi 300 km. Jednocześnie ruszają dwa pociągi: z A osobowy, jadący cały czas z prędkością 60 km/h  do B oraz pospieszny z B do A , jadący z prędkością 100 km/h. O której godzinie się mina?
2. O godzinie 8.00 z A wyrusza do B, oddalonego o 300 km pociąg osobowy jadący cały czas z prędkością 60 km/h . O godzinie 9.00 rusza z A do B pociąg pospieszny jadąc z prędkością 100 km /h. O której godzinie dogoni on pociąg osobowy?
3. Motorówka z Kędzierzyna  płynie do Wrocławia 6 godz. Pod prąd, z Wrocławia do Kędzierzyna 8 godz. Jak długo będzie płynąć słomka Odrą z Kędzierzyna do Wrocławia?

Odpowiedzi:

1. Załóżmy, że pociąg osobowy w momencie mijania się z pociągiem pospiesznym zdążył przejechać drogę s. Wtedy pospieszny przejechał 300-s.
   Przypominam podstawowy wzór dla ruchu jednostajnego droga, s, równa się czas przebycia tej drogi, t, razy prędkość,v, z jaka ta droga została przebyta. s=v*t
   
   Napiszmy równanie wyrażające drogę, prędkość i czas dla obu pociągów w momencie mijania się:
   
   s=60*t  oraz 300-s=100*t. Dodając stronami oba równania mamy   s+300-s=60*t+100*t, czyli 300=160*t . Obliczmy t=300/160=30/16=15/8=7,5/4=112,5/60= 1 godz 52,5 min.
   
   
2. Napiszmy równanie drogi w momencie dogonienia dla pociągu osobowego: s=60*t, dla pospiesznego s=100*(t-1). Drogi przebyte są równe, wiec można przyrównać prawe strony 60*t=100*(t-1), stąd t=2,5
   
   
3. Niech droga Wrocław-Kędzierzyn ma długość s. Wtedy równanie drogi dla słomki, to s=v*t, gdzie v- to prędkość nurtu Odry.
   
   Jak wygląda równanie drogi dla motorówki płynącej z prądem? s=(w+v)*6, w- prędkość własna motorówki, ale w tym wypadku Odra wspomaga motorówkę, wiec prędkości motorówki i nurtu Odry sumujemy. Jeśli motorówka płynie pod prąd, to Odra przeszkadza w ruchu kajaka, motorówka porusza się z prędkością w-v. Równanie ruchu dla motorówki pod prąd, to s=(w-v)*8.
   Ponieważ po lewej stronie mamy to samo wyrażenie s, więc prawe strony też można przyrównać. (w+v)*6=(w-v)*8. Dalej mamy 6*w+6*v=8*w-8*v. Stąd 14*v=2*w, więc w=7*v. Podstawmy do równania drogi dla motorówki płynącej z prądem s=(w+v)*6=(7*v+v)*6=8*v*6=48*v.
   Równanie dla słomki było s=v*t, a my dostaliśmy równanie s=v*48, więc t=48.
   
   Odpowiedź: 48 godzin.

Zadania z fizyki przygotowana przez Kamila Braksatora, nauczyciela z IX LO we Wrocławiu. 

Posłuchaj:

Zadania:

Odpowiedzi:

Zadanie dla Słuchaczy na 22 kwietnia:

Szedł diabeł na spacer, przechodził przez most. Miał w kieszeni pewną sumę pieniędzy. Przechodząc przez ten most wyjął 2 złote, wrzucił do wody. To, co zostało w kieszeni podwoiło mu się. Za jakiś czas wracał, znowu wyciągnął 2 zł, wrzucił do wody, to, co zostało w kieszeni podwoiło mu się. Trzeci raz przechodząc przez ten most wyjął 2 zł, wrzucił do wody, ale niestety już mu nic nie zostało, nie miało się co podwoić. Ile miał pieniędzy na początku?

Najpierw przepytaliśmy celebrytów i Słuchaczy:

Odpowiedź to 3,5 zł. Dlaczego? Posłuchaj:

Zadania z matematyki, które przygotował Zbigniew Lis, nauczyciel matematyki z IX LO we Wrocławiu:

Zadanie 1. Mamy 10 kg 20-procentowego roztworu soli . Ile wody trzeba dolać, aby stężenie soli zmalało do 30%?

Rozwiązanie:

x-waga dolanej wody

(2+x)/(10+x)=3/10. Stąd x=10/7

Zadanie 2. Stężenie soku malinowego wynosi 40%. Ile trzeba dolać wody, aby otrzymać 12 kg soku 30-procentowego?

Rozwiązanie:

x- waga wyjściowego roztworu

(0,4x)/12=0,3 stąd x=9. A zatem trzeba dolać 12-9=3 kg wody.

Zadanie 3. Zmieszano cukierki czekoladowe w cenie 40 zł/kg z cukierkami owocowymi w cenie 20 zł/kg. Otrzymano mieszankę kosztującą 25 zł/kg. W jakim stosunku wagowym zmieszano cukierki?

Rozwiązanie:

X - waga cukierków czekoladowych, y - waga owocowych.

(40x+20y)/(x+y)=25. Z tego otrzymujemy po przekształceniach x/y=1/3.

To znaczy, że trzy razy więcej w mieszance ważą cukierki owocowe.

Zadanie 4. Uzasadnij, że liczba 2^58 + 3^24 jest podzielna przez 5.

Rozwiązanie:

Gdy podnosimy 2 do kolejnych potęg , otrzymujemy takie ostatnie cyfry tych potęg 2,4,8,6,2,4,8,6,2,4,8,6..... Więc co cztery powtarzają się cyfry, na 58 miejscu wypadnie 58: 4= 14 reszty 2, czyli 4.

Podobnie 3 do kolejnych potęg da 3,9,7,1,3,9,7,1,..... Znów widzimy, że cyfry powtarzają się co cztery. Zatem 3^24 ma na końcu 24:4=0, bez reszty, więc na końcu będzie 1.

Gdy się doda dwie liczby naturalne, jedna ma końcówkę 4, a druga 1, to suma ma na końcu 5. To oznacza, że liczba dzieli się przez 5.

Zadania z fizyki dot. pól grawitacyjnych przygotował Kamil Braksator, nauczyciel z IX LO we Wrocławiu:

Zadanie 1. Podaj, jak zmieni się wartość siły przyciągania dwóch jednorodnych kul, jeżeli:

1. Odległość między ich środkami wzrośnie 6 razy
2. Odległość między ich środkami zmaleje 3 razy
3. Masa jednej z kul wzrośnie 2 razy
4. Masa jednej z kul zmaleje 3 razy
5. Masa jednej z kul wzrośnie 2 razy i masa drugiej kuli wzrośnie 3 razy
6. Masa jednej z kul wzrośnie 6 razy a masa drugiej kuli zmaleje 2 razy
7. Masa jednej z kul wzrośnie 2 razy, masa drugiej kuli wzrośnie 2 razy, odległość między ich środkami wzrośnie 2 razy
8. Masa jednej z kul wzrośnie 10 razy, a odległość między środkami kul zmaleje 10 razy

Zadanie 2. Oblicz czas, po którym spadające swobodnie ciało osiągnie 100 km/h. Wynik porównamy z osiągnięciami samochodów kilku wybranych marek.

Zadanie 3. Gdyby udało się umieścić ciało w środku Ziemi, to jaka byłaby wartość siły działającej na to ciało?

Zadanie 4. Jaka jest w przybliżeniu wartość przyspieszenia ziemskiego na wysokości h nad Ziemią, jeżeli h jest równe promieniowi Ziemi?

Odpowiedź do zadania 1.

Każde dwa ciała przyciągają się wzajemnie siłami grawitacji. Wartość siły grawitacji, którą przyciągają się dwie jednorodne kule (lub ciała, które można uważać za punkty materialne), jest wprost proporcjonalna do iloczynu ich mas i odwrotnie proporcjonalna do kwadratu odległości między ich środkami.

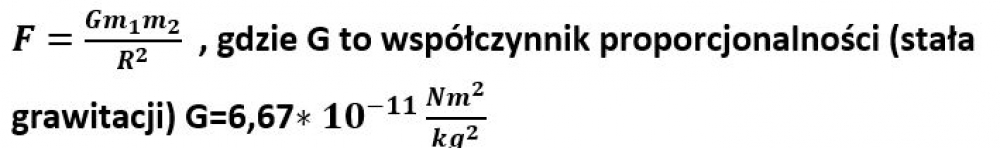
1. Siła maleje 36 razy
2. Siła wzrośnie 9 razy
3. Siła rośnie 2 razy
4. Siła maleje 3 razy
5. Siła wzrośnie 6 razy
6. Siła wzrośnie 3 razy
7. Siła bez zmian
8. Siła wzrośnie 1000 razy

Odpowiedź do zadania 2.

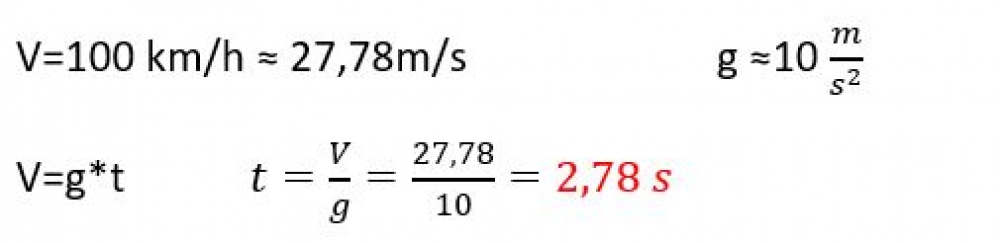
Przykładowe samochody/Czas rozpędzania od 0 do 100 km/h

1. AUDI A8 D4 S8 Facelifting 4.0 TFSI / 3,60 s
2. Mercedes klasa S W222 limuzyna, wersja długa 350 Blue TEC / 7,20 s
3. Fiat 126 Maluch / 51,0 s
4. Volkswagen Polo III / 21,4 s

Odpowiedź do zadania 3

Na ciało umieszczone w środku Ziemi działają we wszystkich kierunkach siły o jednakowych wartościach, równoważąc się. Wypadkowa tych sił jest równa 0.

Odpowiedź do zadania 4

Na wysokości h=Rz, odległość od środka Ziemi d=2Rz. Przyspieszenie ziemskie jest równe w przybliżeniu maleje z kwadratem odległości od środka Ziemi. Stąd przy dwukrotnym zwiększeniu odległości od środka Ziemi, przyspieszenie ziemskie zmaleje 4-krotnie, czyli wyniesie ono około 2,5 m/s2

Oto zadanie dla Słuchaczy, które przygotowaliśmy na 15 kwietnia:

Cegła waży 1 kilogram i pół cegły.

Ile waży cegła?

Zadanie nie sprawiło kłopotów Słuchaczom, także celebryci sobie poradzili:

Odp. Cegła waży 2 kilogramy. 

ZAJĘCIA Z 15 KWIETNIA:

Kamil Braksator, nauczyciel fizyki z IX LO im. J. Słowackiego we Wrocławiu, przygotował kolejną lekcje:

Zbigniew Lis - nauczyciel matematyki w IX LO, także tłumaczył różne zagadnienia Słuchaczom:

ZAJĘCIA Z 8 KWIETNIA:

Gdy skończył się koronawirus i wreszcie można było iść do parku na polanie spotkali się ludzie ze swoimi psami. Ilu było opiekunów, ile opiekunek o ile psów jeśli wiemy, że były 62 głowy, 12 tuszy do rzęs i 206 nóg?

Jak zwykle najpierw zapytaliśmy o zdanie celebrytów. Z zadaniem zmierzyli się komik Michał Paszczyk, aktora Magdalena Kumorek, a także muzyk Mesajah:

Zbigniew Lis- nauczyciel matematyki w IX LO we Wrocławiu wszystko wyjaśnił:

Zajęcia 8 kwietnia zaczęliśmy od fizyki. Kamil Braksator, nauczyciela fizyki z IX LO im. J. Słowackiego we Wrocławiu, przygotował lekcje i zadania.

Posłuchaj:

cz.1. 

cz.2.

Oto zadania:

Zasady zachowania:

1. Dziewczynka trzyma piłkę na wysokości 1 m nad ziemią i rzuca ją pionowo w górę z szybkością początkową 4. Oblicz z jaką szybkością piłka uderzy o ziemię. Przyjmij g=10. Pomijamy opory powietrza.

   Na jaką maksymalną wysokość wzniesie się piłka nad powierzchnią ziemi?

2. Z jaką szybkością po wystrzale odskoczy do tyłu karabin o masie m₁= 5 kg, jeżeli masa wystrzelonego pocisku m₂=0,01 kg, a jego szybkość początkowa v₀=500

3. Z pośród wymienionych wielkości fizycznych, wybierz te wielkości, które są zachowane dla każdego z przedstawionych poniżej rodzajów zderzeń. Wstaw znak X w odpowiednie miejsce.

Wielkości fizyczne:

1. Pęd całkowity

2. Prędkość

3. Energia kinetyczna

4. Energia całkowita

		a	b	c	d
1	Zderzenia sprężyste
2	Zderzenia niesprężyste

Termodynamika i własności materii

Zadanie 1. (informator maturalny 2015 r.)Czarna herbata smakuje najlepiej, gdy zalejemy ją wodą o temperaturze ok. 100 oC. Herbata zaparzona na Mount Everest (m n.p.m) smakuje gorzej. Dokończ poniższe zdanie tak, aby było poprawne. Wybierz odpowiedź (A lub B) i jej uzasadnienie (1 lub 2). Wstaw znak X w odpowiednim miejscu.

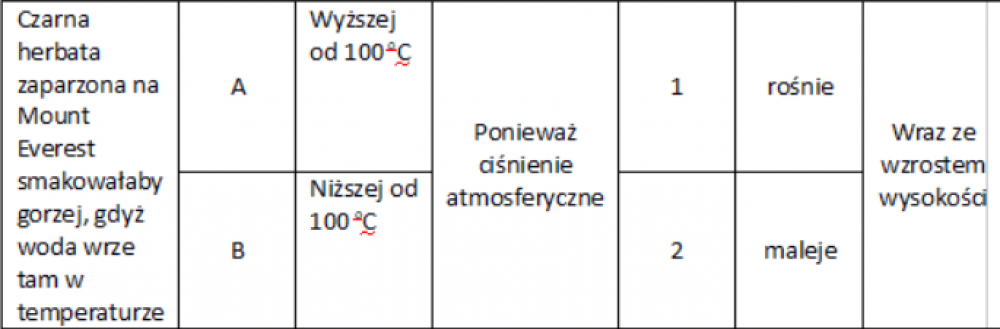
Zadanie 2. Jaka jest różnica między parowaniem a wrzeniem?

Odpowiedź do zadania 1 (zasady zachowania)

+mgH =

Odpowiedź do zadania domowego 1 (zasady zachowania)

+mgH =mg
+H

Odpowiedź do zadania 2 (zasady zachowania)=1

Odpowiedź do zadania 3 (zasady zachowania)

		a	b	c	d
1	Zderzenia sprężyste	x		x	x
2	Zderzenia niesprężyste	x			x

Odpowiedź do zadania 1 (termodynamika i własności materii)

Odpowiedź do zadania 2 (termodynamika i własności materii).

Odp. Parowanie następuje z powierzchni cieczy, natomiast wrzenie zachodzi w całej objętości cieczy w konkretnej temperaturze wrzenia.

STATYSTYKA - lekcja matematyki na 8 kwietnia

Posłuchaj:

ZADANIE:

Spytano 10 małżeństw, ile maja dzieci. Oto odpowiedzi 3,2,3,3,4,2,1,1,0,2. Podaj dominantę, medianę, odchylenie standardowe tych danych. Jaka liczba dzieci posiadanych przez te małżeństwa jest typowa, tzn. jest odchylona od średniej o mniej niż jedno odchylenie standardowe?

ROZWIĄZANIE:

0,1,1,2,2,2,3,3,3,4. Mediana to 2, dominanty to 2 i 3, średnia 2,1, a odchylenie standardowe to ok.1,14. Ile danych mieści się w przedziale 1,07 do 3,35? Tylko 6.

A oto matematyczna zadania na 1 kwietnia.

1.
Lecą pszczoły na kwietna łąkę w szyku po 2, 3, 4, 5, 6, i 7. Zawsze jedna z nich jest samotna. Jaka minimalna liczbę pszczół liczy sobie ten rój?

Rozwiązanie:

Znajdujemy najmniejszą wspólną wielokrotność liczb 2,3,4,5,6,7. Jest to 420. Zatem odpowiedź do zadania to 421.

2.
Czy trójkąt może mieć wysokości 1,2,3?

Rozwiązanie:

Wtedy a=2b=3c. Stad b=a/2, c=a/3. Zatem a/2+a/3=7a/12<a, czyli taki trójkąt nie istnieje.

3.
Czy trójkąt może mieć wysokości 2,4,5?

Rozwiązanie:

Wtedy 2a=4b=5c. Stad b=a/2 ,c=2a/5. Suma krótszych wysokości to

2a/5+a/2=9a/10<a. Trójkąt nie istnieje.

4. 
Jak policzyć pole trójkąta mając trzy jego wysokości? Np. 2,3,4?

P=2a/2=3b/2=4c/2. stad b=2a/3,c=a/2.Dalej a=P, b=2P/3, c=P/2
Policzmy połowę obwodu p=13P/12.

Wzór Herona: P=sqrt(p*(p-a)*(p-b)*(p-c))
Wstawiamy wyliczone wartości do wzoru.

P=144/sqrt(455)
Sqrt to pierwiastek kwadratowy

Istnienie trójkąta omawiał Zbigniew Lis:

Pierwszy kwietniowy program zaczęliśmy od zadania od naszej Słuchaczki:

W czasach przed koronawirusem grupa uczniów idzie na wycieczkę. Gdy ustawili się w pary, trójki i czwórki za każdym razem jeden został bez pary. Dopiero gdy ustawili się po pięciu nikt nie pozostał sam.

Ilu było uczniów w grupie?

Trudne? Zapytaliśmy naszych Słuchaczy, ale nie tylko, bo także z zadaniami zmierzyli się konferansjer i komik Piotr Gumulec, himalaista Rafał Fronia, a także dyrektor Karkonoskiego Parku Narodowego Andrzej Raj.

Posłuchajcie:

Większość Słuchaczy podała dobrą odpowiedź. To 25. Dlaczego? Tłumaczył Zbigniew Lis:

Zadania Zbigniewa Lisa, matematyka z IX LO i. J. Słowackiego we Wrocławiu:

1. Jeśli jeden pracownik wykona prace w 10 godzin, drugi w 15 godzin, a trzeci w 30 godzin , to w jakim czasie wykonają te prace razem?

Odpowiedź: 5 godzin 

2. Pierwszy pracownik, który wykonuje sam te prace w ciągu 10 godzin, zaczął je wykonywać o godzinie 8.00, drugi , który sam wykonuje te prace w ciągu 15 godzin, dołączył o godzinie 9.00. O której praca zostanie zakończona?

Odpowiedź:  o godzinie 14.24  

3. Jakie jest prawdopodobieństwo, ze rzucając pięcioma kostkami otrzymamy karetę, czyli taki układ, w którym dokładnie cztery razy występuje ta sama liczba oczek?

Odpowiedź: 150/7776, czyli ok. 1,93%

Potrzebujecie podpowiedzi? Posłuchajcie: 

Lekcja Fizyki przygotowana przez Kamila Braksatora, nauczyciela fizyki z IX LO im. J. Słowackiego we Wrocławiu.

Zadanie omawiane 25.03.2020: (1. Mechanika punktu materialnego i bryły sztywnej)

Na platformie ciężarówki spoczywa skrzynia o masie 100 kg. Ciężarówka porusza się poziomo, ruchem jednostajnie przyspieszonym z przyspieszeniem 2 m/s2

Pytania:

Oceń prawdziwość poniższych zdań:

1)      Wartość siły nacisku, jaką skrzynia wywiera na podłoże przyczepy, jest równa ciężarowi skrzyni. PRAWDA

2)      Skrzynie umieszczamy w windzie. Winda stoi w miejscu. Wartość siły nacisku, jaką skrzynia wywiera na podłoże, jest równa ciężarowi skrzyni. PRAWDA

3)      Skrzynie umieszczamy w windzie. Winda  porusza się ze stałą prędkością w górę lub w dół. Wartość siły nacisku, jaką skrzynia wywiera na podłoże, jest równa ciężarowi skrzyni. PRAWDA

4)      Skrzynie umieszczamy w windzie. Winda  porusza się w górę lub w dół z przyspieszeniem zwróconym w górę. Wartość siły nacisku, jaką skrzynia wywiera na podłoże, jest równa ciężarowi skrzyni. FAŁSZ.  Komentarz: siła nacisku ma większą wartość od ciężaru.

5)      Skrzynie umieszczamy w windzie. Winda  porusza się w górę lub w dół z przyspieszeniem zwróconym w dół. Wartość siły nacisku, jaką skrzynia wywiera na podłoże, jest równa ciężarowi skrzyni. FAŁSZ.  Komentarz: siła nacisku ma mniejszą wartość od ciężaru.

Zadanie domowe:

Skrzynie umieszczamy w windzie. Winda  spada swobodnie z przyspieszeniem grawitacyjnym. Wartość siły nacisku, jaką skrzynia wywiera na podłoże, jest równa ciężarowi skrzyni.

Odpowiedź poprawna:

FAŁSZ.

Komentarz: Brak siły nacisku. Stan zbliżony do stanu nieważkości.

Korki zDolnego Śląska - nasi dziennikarze zmierzą się z waszymi pytaniami. Jak nie dadzą rady, wtedy zapytamy najlepszych dolnośląskich nauczycieli w środowym programie Reakcja24. Wtedy też przedstawimy następne zadania dla Was!

Pytaj całą dobę [email protected], telefonicznie 71 339 90 60 lub przez formularz. Szukaj odpowiedzi w środę między godziną 9.00 a 16.00, zwłaszcza w programie Reakcja24 po 12. 00.